Stell Dir vor Du bist in einer Gameshow und hast es bis zu dem Punkt geschafft, wo der Moderator Dich fragt für welches Tor Du Dich denn nun entscheiden möchtest. !, 2 oder 3 steht zur Auswahl und nur hinter einem Tor befindet sich das Auto, hinter den beiden Anderen nur Nieten. Du entscheidest Dich also für ein Tor und der Moderator öffnet ein anderes um zu zeigen das sich hinter dem anderen eine Niete befindet und stellt Dich for die Wahl: „Willst Du bei Deinem Tor bleiben oder lieber wechseln“.
Nun ist die große Frage ob es geschicker ist zu wechseln, bei Deinem Tor zu bleiben oder ob es egal ist.
Der gesunde Menschverstand sagt zunächst das sich an der Wahrscheinlichkeit nichts ändert, da man ja jetzt eine 50/50 Chance hat das Auto zu bekommen und es daher egal ist ob man wechselt oder bei seinem Tor bleibt.
Diese Frage wurde scheinbar schon oft diskutiert und hat den Namen „Das Monty Hall Problem“ bekommen, da die „Monty Hall Show“ in Amerika wohl die erste Show war die mit diesen 3 Toren gearbeitet hat. Mark Evanier, Comicschreiber und ein guter Freund von Steve Gerber hat in den letzten Tagen mehrfach versucht zu erklären wie das ganze zu erklären ist. Ich versuche es hier mal in Deutsch:
Zunächst schauen wir uns an was passiert wenn der Kandidat nicht wechselt. In der ersten Spalte ist die erste Wahl des Kandidaten, in der zweiten das Tor hinter dem sich das Auto befindet und in der dritten das Ergebniss.
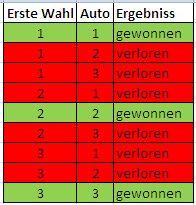
Man kann gut erkennen das der Kandidat nur in 3 von 9 Fällen das Auto gewinnt, sollte er bei seiner Entscheidung bleiben.
Schauen wir uns nun die selbe Tabelle an, nur diesmal wechselt der Kandidat auf ein anderes Tor:
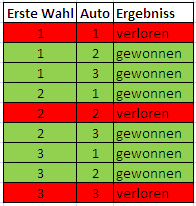
Hier nun gewinnt der Kandidat in 6 von 9 Fällen das Auto.
So seltsam es sich anhören mag, es ist in diesen Fällen immer besser das Tor zu wechseln. Die Erklärungen in der Wikipedia sind auch sehr hilfreich, vor allem dieser Satz ist doch sehr eindrücklich:
Der Moderator kann nur ein Tor öffnen, hinter dem sich der Gewinn nicht befindet. Er muss in der hier besprochenen Aufgabenstellung immer ein Tor wählen. Ein Kandidat, der sich immer gegen den Wechsel entscheidet, gewinnt nur, wenn er auf Anhieb das richtige Tor trifft. Dies geschieht in einem Drittel der Fälle. Ein Kandidat, der immer wechselt, verliert in allen Fällen, in denen er ohne Wechsel gewonnen hätte, also einem Drittel der Fälle, und gewinnt folglich in zwei Dritteln der Fälle.
